GOLD
FORECAST REPORT OPTION OF SIRIUS
A
forecast of gold prices was developed in 2006 and
is available
as the “Gold Forecast” report
option of the Sirius astrology program. This gold forecast
is based on minor aspects, also sometimes referred
to as harmonic aspects or harmonics. It produces a
strong correlation of predicted gold prices and actual
gold prices (see http://astrosoftware.com/goldforecast.htm).
The
statistical analysis performed however may have given
biased or inaccurate results for two reasons:
(1)
Failure to adjust calculations based on different
starting dates and
(2) A meta-analysis using
a rarely used statistical software package.
These
two
issues
are addressed in a reanalysis of the gold forecast,
and the new analysis confirms the previous
findings. This confirmation of the earlier analysis
may
represent one of the strongest validations of a
measurable effect of astrological variables, especially
given
the recent
reanalysis of Gauquelin studies which suggest
that there are limitations and problems in the
Gauquelin
research that were previously unidentified.
Click on the links below to view the articles.
The
Gold Forecast report option of Sirius predicts relatively
short-term forecasts of gold prices. Gold
prices from January 1, 1975 to June 30, 2006 were analyzed.
The forecast produces relatively short-term forecasts
based on the angular relationship of the geocentric
positions of the planets measured along the ecliptic
plane.
For
example, Sun and Jupiter in 7th harmonic aspect
aspect is one of the predictors of higher
gold prices.
The 7th harmonic aspects are 1/7, 2/7, and 3/7
of the circle, which is equivalent to 51 3/7, 102
6/7,
and 154 2/7 degrees. Whether
the Sun is ahead of behind of Jupiter does not matter. One
can also regard the angles as 1/7, 2/7, 3/7, 4/7, 5/7, and
6/7 of the circle as the Sun proceeds
moves in its synodic cycle with Jupiter returning back to conjunction
to Jupiter approximately every 13 months. The
0/7 aspect,
or conjunction, was not included
as a 7th harmonic aspect in the formula.
The
forecast based on Sun and Jupiter in 7th harmonic
produces an expected
rise
in gold prices approximately every
seven weeks with one exception: when the Sun is 6/7 of the circle
past Jupiter and the conjunction is “jumped over” and
the next peak is predicted to occur when the
Sun is 1/7 past Jupiter and thus there are approximately
14 weeks between the occurrence of the 6/7 and 1/7 aspect.
There
are six predicted
rises in gold prices (the 1/7, 2/7, 3/7, 4/7, 5/7, and 6/7 aspects
of
Sun and Jupiter) which occur over a period
of about 13 months. An orb of slightly less
than two degrees is allowed and each rise in gold prices is therefore
forecasted to last about four days. All durations
vary because the speeds of planets vary
over time.
The forecast based on 7th harmonic aspects of Sun and Jupiter is simple and
elegant. The predicted gold price is predicted to begin rising as Sun and
Jupiter are within two degrees of one of these six aspects, the gold price
reaches
its peak when the aspect is exact, and the price declines as the planets
separate from each other by about a 2 degree orb again. The predicted rise
and fall
of gold prices over these time periods of approximately four days is expected
to conform to a gradual increase similar to a sine wave. There are no autoregressive
effects or other effects based on a cyclic analysis or the effect of earlier
prices on later prices. There are also no time delays in the effect of the
astrological variable.
In
the terminology used by research methodologists,
the astrological influence is an extraneous time-varying
covariate. The astrological
variable is clearly extraneous because planetary orbits are determined
by mathematical formulae that are independent of
human behavior.
Another
elegant feature of
this forecast is that all 7th harmonic aspects are given equal
weight. The 1/7 aspect, for example, is expected
to increase
gold prices by the same
amount as a 2/7 aspect and 3/7 aspect would. All of the harmonic
aspects are also
given the same orb. The theoretical framework for this study is
harmonic astrology as described by John Addey and
specific interpretations
elaborated by David
Cochrane. In harmonic astrology, angles between planets that are
within orb of a fraction have a similar, but not
identical, effect if that aspect expressed
as a fraction has the same denominator. This expectation is based
on the concept that astrological aspects operate
through a kind of wave function
that has
as yet been undetected by any instruments.
Gold
prices are posted on daily trading days, which are
weekdays except major
holidays. There are consequently about 255 trading
days each
year. A forecasted
price can be produced for every day of the year but gold prices
are given only on trading days. This issue can be viewed as a
missing data problem
in that
gold prices would be available every day if the services were
provided to give gold prices as people will buy and
sell gold every day
and
virtually all of
the forces that affect gold prices are in effect on weekends
as well. As a crude analogy, one might say that a
person still has
a pulse
even if
the
pulse
is not measured. The “missing” gold prices can be
ignored or imputed. We can get a sense of the effects of missing
gold prices
by looking
at a graph
of actual and predicted gold prices over a 3-month period with
the missing gold prices imputed, as shown in Figure 1.
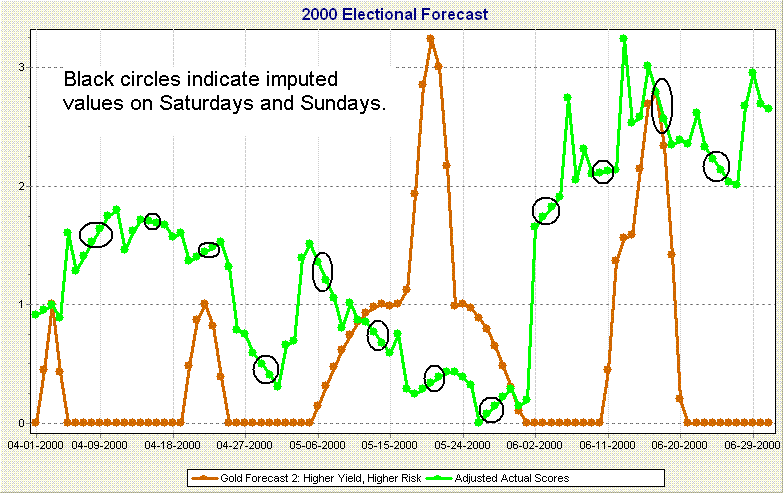
Figure
1. 3-Month Forecast with Imputed Values on Weekends
Identified
As
shown in Figure 1, the imputed values for days on
non-trading days, are values that are determined
by a simple linear interpolation between the prices
on the preceding Friday and following Monday. Over
the 3-month period the linear interpolation used to
impute values for weekends appears to be reasonable.
Given that the price of gold must change from its price
on Friday to its price on Monday, the assumption of
a steady linear change over Saturday and Sunday is
reasonable and represents the likely mean values if
prices varied randomly from the price on Friday to
the price on Monday. As can be seen by looking at the
graph in Figure 1, the amount of deviation that is
likely from these imputed prices is not likely to drastically
change the overall relationship of the predicted prices
(red line) to the actual prices (green line). For this
analysis we used imputed values of the gold prices
on non-trading days, a shown in Figure 1.
Note
that the predicted prices shown in Figure 1 are based
on more astrological factors than the Sun-Jupiter
7th harmonic aspects. A Sun-Jupiter 7th harmonic
aspect is likely to occur only one time on average over the three month period
so there would be only one predicted period of about 4 days when prices would
increase if only Sun-Jupiter aspects were used to predict a rise in gold prices.
There
are two gold forecasts produced by the Gold Forecast
report option of Sirius. One of these forecasts
is called the “Higher Yield, Higher Risk” forecast
because the mean correlation based on this formula is higher than the other
forecast but the range of correlations is also
greater. The difference between the mean,
minimum, and maximum correlations between the two forecasts is not great.
In the present study only the Higher Yield, Higher
Risk forecast is analyzed.
In
retrospect, the Lower Yield, Lower Risk forecast
is arguably a better
candidate for research because the collection of astrological variables
are more consistent,
i.e., they are simpler and more elegant than the variables used in the
Higher Yield, Higher Risk forecast. Both forecasts
have 36 items, and 7 of the 36
items are harmonic aspects, while the other 29 items are asymmetric isotraps
(explained
below). The 7 harmonic aspects in the Lower Yield, Lower Risk formula are
between Sun and Jupiter or Jupiter and Neptune and are 7-based harmonics
or conjunctions.
The 7-based aspects are harmonics 14, 21, 28, and 35 between Sun and Jupiter.
The Higher Yield, Higher Risk formula also includes 5th harmonic aspects
between Venus and Mars and between Mars and Jupiter, a trine aspect between
Sun and
Saturn and therefore uses more planets in more harmonics than the Lower
Yield, Lower
Risk formula.
In
the future a replication of the current study with
the Lower Yield, Lower Risk formula is planned and
similar
results are expected because
the differences in mean, minimum, and maximum correlations using the
two formulae are small, and the lower risk of the
Lower Yield, Lower Risk formula
compensates
to some extent for the lower correlations because the correlations are
more consistently positive and thus there is likely
less variability in the correlations.
In
addition to harmonic aspects, both formulae use midpoint-to-midpoint
aspects as predictors.
More specifically, 18th harmonic midpoint-to-midpoint
aspects
between Sun, Mars, Jupiter, and Uranus and 3rd and 6th harmonic midpoint-to-midpoint
aspects between Mars, Jupiter, Uranus, and Neptune are used as predictors.
Midpoint-to-midpoint relationships are regarded as highly important
in
the theoretical framework of
symmetrical astrology. Cochrane has written extensively about their
importance in compatibility and in relationship to
arabic parts. See, for example,
http://www.astrosoftware.com/Symmetries.htm and http://www.astrosoftware.com/ArabicParts.htm).
STATISTICAL
ANALYSIS: Meta-analysis of 3-month
Periods
As
discussed above, the model for the gold forecast
is elegant and simple. The only variables are extraneous
time-varying covariates that affect the dependent variable
(gold prices) without any time delay. There are not
any autoregressive or cyclic effects that are considered
in this study. There is, however, one issue in the
statistical analysis that presents an obstacle: how
to measure the effect of a time-varying covariate that
is expected to have an effect for a relatively short
period of time over time series data that extends for
a relatively long period of time. In this case there
are 31 ½ years of gold data and each of the
time-varying covariates (the astrological variables)
is expected to affect gold prices over a period of
a few days to a few weeks. If gold prices were relatively
stable over the 31 years, the long-term effects would
not overwhelm short-term trends but gold prices, like
many financial measures and indicators, have very dramatic
long-term trends. Gold prices may, for example, go
up or down in a striking manner over a period of months
or years. These larger trends overwhelm the short term
effects in a correlation that spans the entire 31 years.
The graph in Figure 2 demonstrates the problem.
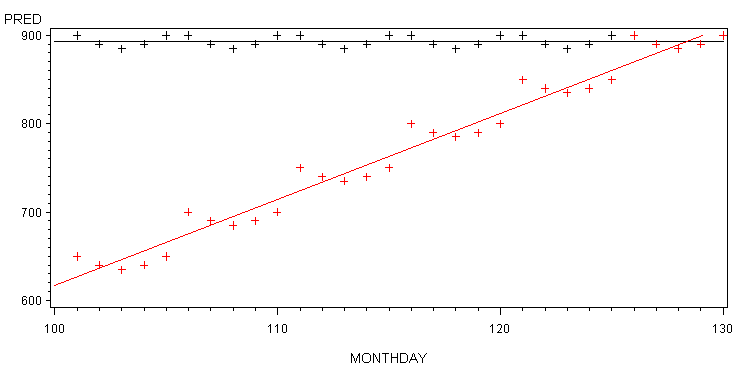
Figure 2: Example of Short-Term Forecast Overwhelmed
by Long-Term Trend
The
red “+” characters in Figure
2 represent the actual data. The linear fit to this data
is shown by the red line. The black “+” characters
near the top of the graph represent the predicted values
based on an extraneous time-varying covariate that is
able to only forecast behavior in relationship to the
random expected behavior over a short period of time.
A horizontal regression line is drawn through these forecasted
values. Notice that the forecasted values are perfect.
The actual values are grouped in a series of five values
that starts high goes gradually down to the third value
of the five and then back up. If we divide the data into
6 separate analyses of 5 values each, then the r correlation
coefficient will be a perfect 1.0. However, the r correlation
coefficient for the data in this graph is only .07 and
the p value is .71 indicating that our predicted values
have no relationship to the actual values. The horizontal
black regression line for predicted values and the ascending
red regression line of actual values reinforces this
point. The predicted values do not do a very good job
of correlating with actual values even though over a
5-day period the correlation is perfect.
For
the interest of anyone who may wish to “play” with
this issue, the SAS code to generate the above graph
is given in Table 1.
Table 1. SAS Code that generates the data
in Figure 2.
options ps=60 ls=78;
Data One;
INPUT MONTHDAY 1-4 ACTUAL 6-8 PRED 10-12;
DATALINES;
0101 650 900
0102 640 890
0103 635 885
0104 640 890
0105 650 900
0106 700 900
0107 690 890
0108 685 885
0109 690 890
0110 700 900
0111 750 900
0112 740 890
0113 735 885
0114 740 890
0115 750 900
0116 800 900
0117 790 890
0118 785 885
0119 790 890
0120 800 900
0121 850 900
0122 840 890
0123 835 885
0124 840 890
0125 850 900
0126 900 900
0127 890 890
0128 885 885
0129 890 890
0130 900 900
* PROC PRINT;
SYMBOL1 V=plus C=black I=R;
SYMBOL2 V=plus C=red I=R;
PROC GPLOT DATA=ONE; PLOT (PRED ACTUAL) * MONTHDAY /OVERLAY;
PROC CORR DATA=ONE SSCP CSSCP COV;
RUN;
QUIT;
To
summarize, the detection of short-term effects of extraneous
time-varying
covariates over time series data over a relatively long
period of time is overwhelmed by strong long-term trends
in the data. The strong long-term trend in the data in
Figure 2 is the positive trend upwards over time. Although
the data in Figure 2 is idealized in order to illustrate
the point, the same principles are in effect in the analysis
of the astrological variables used in the gold forecast.
Three
possible ways to address this issue come to mind:
(1) Find astrological variables that predict long-term
trends so that the complete forecast is possible.
This option is theoretically unattractive to me because I doubt that astrological
variables have a clear association with long term trends as these trends
are most likely affected by a complex interaction of
a great many variables, including
social policies in various countries, overall economic trends, etc.
(2) A
kind of correction for long-term effects may be possible.
For example, in the idealized
data in Figure 2, the data could be corrected for the linear effect. However,
with complex real-world data, establishing a sound procedure for a correction
factor would be extremely complex.
(3) Divide the data into smaller sections
of time and obtain a set of correlation values. This approach is intuitively
appealing because the theory proposed is that short-term trends can be predicted
so dividing the data into groups of short-term trends reflects clearly and
directly
the hypothesis being proposed.
One
might expect that the best statistical procedures for
analyzing this data would be clearly presented
in books and research papers. However, after a thorough
search through a great many online sources of books on time line series and
longitudinal data analysis, and a search for relevant papers in research
journals, I was unable
to find one that addressed this issue. Not having expertise in this particular
area of research methodology, I may have easily overlooked this information.
The difficulty in locating this information may be surprising in that the
issue seems simple, basic, and straightforward while
much more complex issues are
addressed in time series analysis, but it is perhaps not surprising in that
research methods
are typically developed out of real-world needs. Much of the progress in
time series analysis and longitudinal data analysis
evolves from issues encountered
in medical, economic, and educational studies. Encountering an analogous
situation where an extraneous time-varying covariate
has short-term effects that are
overwhelmed by long-term trends in time series data appears to be unlikely.
Research on measurable
effects of astrological variables is not only outside the mainstream of academia
and research institutes but largely outside the mainstream of astrology as
well, which is more focused on issues of personality, qualitative effects,
divination,
and psychic or metaphysical perception rather than measurable effects.
When
the gold forecast option of Sirius was developed
in late 2006, the decision was made to divide the 31 ½ years
of data into 126 3-month periods and thus produce 126
Pearson r correlation values and then analyze the total
effect
of these 126 correlations with a kind of meta-analysis. Even though meta-analysis
is typically associated with obtaining a synthesized result from separate
studies, the assumptions of the meta-analysis statistical
methods are appropriate for
analyzing the 126 correlations produced by the gold forecast. In fact, the
consistency of the data in terms of the manner in which
it is gathered and the similar n
(number of data) in each 3-month period is very consistent with the assumptions
of meta-analysis statistical methods and is less likely to violate the assumptions
of the statistical analysis than a meta-analysis of separate studies.
REANALYSIS
USING DIFFERENT STARTING DATES
Having been
unsuccessful in identifying a precedent for measuring
short-term effects of time-varying covariates
on time series data with strong long-term trends, the
statistical procedure that I used in 2006 appears to
be reasonable. There are two limitations in the analysis
of the data that was performed in 2006 that are addressed
in the current reanalysis of the data:
(1)
In the analysis of the data performed in 2006 the starting
dates of each
3-month period were January 1, April 1, July 1, and
October 1. These are the dates that were used in the
study of
the data to develop the two AstroSignatures (the Low
Yield, Low Risk and High Yield, High Risk sets of astrological
variables). An
analysis needs to be conducted using other starting
points to see if the results are sufficiently
robust to be present when different starting dates.
The gold forecast is the result of exploratory research
rather
than a hypothesis test and the significance level of
the results do not “prove” anything. Rather,
they are used to help guide a path of exploration that
may eventually lead to a definitive finding. Analyzing
the results using different starting dates is a first
step in determining if the findings are generalizable
even at a most basic level. If the statistical significance
is greatly impacted by changing the starting dates,
then the exploratory research has been found to be
ineffective
from the outset.
(2)
The meta-analysis was performed using a rarely used
software program developed by a
professor at the University of Miami primarily
for pedagogical
purposes. The rapid expansion of the R statistical
language system in recent years makes it an attractive
tool. In
this reanalysis of the High Yield, High Risk AstroSignature
developed in 2006, the meta-analysis was performed
using R.
In the reanalysis of the gold data, 126 correlations
between the predicted and actual gold prices were produced
using the Sirius 1.2 software. In Sirius 1.2 a new feature
has been added to allow automatic saving to file of all
126 analyses with results saved to file in a CSV file
that can be used by R code, other statistical software,
and spreadsheet software. The analysis was repeated with
different starting dates separated by 10 to 15 days.
In Table 2 the starting dates in the first quarter of
each year, the p value and mean r correlation value are
given. The other starting dates are on the same day of
the month every 4 months so that, for example, for the
data beginning on February 26, correlations are for 3-month
periods beginning February 26, May 26, August 26, and
November 26.
Table 2. Probabilities and Mean Correlation
(r) of Predicted and Actual Gold Prices for Eight Different
Starting Dates of the Gold Forecast
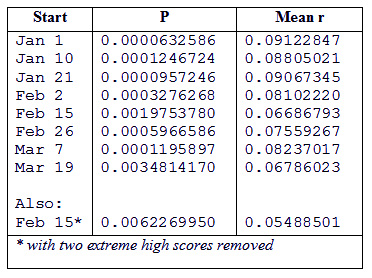 At
the bottom of Table 2 is an additional set of values
for the 3-month period beginning February 15, but with
the highest two correlations removed. The reason for
performing this analysis is evident by inspecting the
graphs in Figure 3. The second graph in Table 3 shows
the 126 correlation values and standard errors. Two of
the 126 correlations were much higher than the other
124, as can be seen in the discontinuous jump from the
previous values in the bottom two r correlation values
shown in this graph. In the third graph is the same data
plotted with these two very high correlations removed.
Note that these correlations are not outliers and should
not be removed! They were removed only for the purpose
of seeing how much affect they had on the mean correlation
and p value for the analysis beginning on February 15.
Note also that mean correlations are slightly different
from a mean value that would be calculated by simply
adding the 126 correlations and dividing by 26. These
are mean values based on the meta-analysis and take into
account the number of dates in each 3 month period, which
varied only slightly between 90 and 92. At
the bottom of Table 2 is an additional set of values
for the 3-month period beginning February 15, but with
the highest two correlations removed. The reason for
performing this analysis is evident by inspecting the
graphs in Figure 3. The second graph in Table 3 shows
the 126 correlation values and standard errors. Two of
the 126 correlations were much higher than the other
124, as can be seen in the discontinuous jump from the
previous values in the bottom two r correlation values
shown in this graph. In the third graph is the same data
plotted with these two very high correlations removed.
Note that these correlations are not outliers and should
not be removed! They were removed only for the purpose
of seeing how much affect they had on the mean correlation
and p value for the analysis beginning on February 15.
Note also that mean correlations are slightly different
from a mean value that would be calculated by simply
adding the 126 correlations and dividing by 26. These
are mean values based on the meta-analysis and take into
account the number of dates in each 3 month period, which
varied only slightly between 90 and 92.
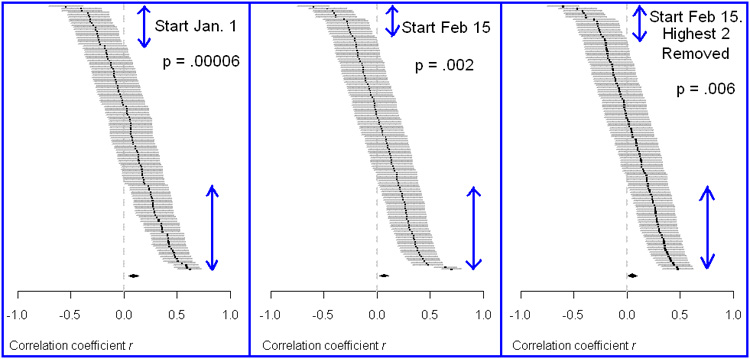
Figure 3. Graph of 126 correlations of 3-month periods
between predicted and expected gold prices.
The gray
lines extending from the correlation values indicates
the standard error of measurement.
The third graph has
the highest two correlations removed so is based on 124
correlations instead of 126.
The
mean r values shown in Table 2 range from .067 to .091.
As expected, the highest correlation
occurs on the dates on which the AstroSignature was developed,
January 1. The correlations did degrade on other dates.
Interestingly, the correlations do not gradually become
worse as the starting date is increased from January
1, although the date farthest from the Jan. 1 / April
1/ July 1/ Oct 1 series does have the lowest mean correlation
of .067 (Feb 15 / May 15/ Aug 15 / Nov 15 series). The
mean correlation is very closely related to the p value,
although they are not simple transformations of each
other because the standard error of measurement also
affects the p value. The lowest p value is .00006 and
the highest p value is .00198. With the two highest correlations
removed the p value went from .00198 to .00348. Thus,
the two high correlations did not have a dramatic effect
on the overall results. Even with them removed, the results
are highly significant.
The
vertical blue lines with arrow heads in Figure 3 show
the areas of p values that are clearly below or above
a random correlation of 0 based on the 95% confidence
intervals. In other words the vertical blue lines are drawn where the grey
lines
do not cross the vertical line that indicates a correlation of 0. The blue
lines are longer for positive correlations than for
negative correlations, as is expected
by the highly significant results. Visuals of data are very important in exploratory
research and these graphs help us to understand what the quantitative results
are telling us.
Table 3. R Code to produce Meta-Analysis
setwd("c:/mypath")
library("metacor")
# execute one line below for data which we want to analyze:
GoldCorrDat <- read.csv(file="GoldStartJan1.txt",head=TRUE,sep=",")
# GoldCorrDat <- read.csv(file="GoldStartJan10.txt",head=TRUE,sep=",")
# GoldCorrDat <- read.csv(file="GoldStartJan21.txt",head=TRUE,sep=",")
# GoldCorrDat <- read.csv(file="GoldStartFeb2.txt",head=TRUE,sep=",")
# GoldCorrDat <- read.csv(file="GoldStartFeb15.txt",head=TRUE,sep=",")
# GoldCorrDat <- read.csv(file="GoldStartFeb26.txt",head=TRUE,sep=",")
# GoldCorrDat <- read.csv(file="GoldStartMar7.txt",head=TRUE,sep=",")
# GoldCorrDat <- read.csv(file="GoldStartMar19.txt",head=TRUE,sep=",")
# GoldCorrDat <- read.csv(file="GoldStartAll4.txt",head=TRUE,sep=",")
# GoldCorrDat <-
# read.csv(file="GoldStartFeb15TwoHighOutliersRemoved.txt",
# head=TRUE,sep=",")
GoldCorrDat <-
GoldCorrDat[order(GoldCorrDat$Corr),]
# sort by correlation
to make plot look nicer
GoldRes <- metacor.DSL(GoldCorrDat$Corr, GoldCorrDat$N, "",
plot=TRUE)
# DerSimonian-Laird method with plot
# variation with dates in plot: GoldRes <-
metacor.DSL(GoldCorrDat$Corr,
GoldCorrDat$N, GoldCorrDat$Date,
plot=TRUE) # DerSimonian-Laird
method with plot
GoldRes
The R code for producing the meta-analysis is given in Table 3. A DerSimonian-Laird
meta-analysis was conducted using the metacor package. The DerSimonian-Laird
meta-analysis is recommended for an analysis of random effects and it is
more conservative than an analysis based on fixed effects. Because the gold
data can be considered a sampling of data from the total population of possible
gold prices and because a conservative test is desired in exploratory research
so that one does not get overly hopeful signals of a possible relationship,
and because the DerSimonian-Laird meta-analysis is generally regarded as
appropriate in social science research, it was selected as the statistical
procedure.
CONCLUSION
This
research study was inspired by a concern that the results
published earlier on the correlations produced
by the gold forecast might be exaggerated by (a) using
an inappropriate model to analyze the data, (b) use of
an unusual statistical package by a researcher who was
very unfamiliar with meta-analysis and had few resources
to determine if the analysis is appropriate, and (c)
failure to use varying start dates instead of only the
start dates of Jan 1/ April 1 / July 1 / Oct 1 which
were also the dates used to develop the gold forecast
AstroSignature.
Given
the tendency of astrological research to fail to produce
measurable results and the recent negative results
obtained by this researcher in the reanalysis
of the Gauquelin data, I was prepared for the worst, so to speak. Contrary
to these concerns and negative expectations, the results were robust under
changes in starting data. The worst p value obtained was .003 which is still
highly significant even though, a expected, less than the .00006 significance
level obtained with the Jan 1 / April 1 / July 1 / Oct 1 starting dates.
Also, using an accepted meta-analysis method (DerSimonian-Laird)
with statistics
software that is widely used in professional journals alleviates concerns
about accuracy of the calculations.
The
research design is in need of review by experts in
time series analysis. Consultation on this matter with
several professors in research methodology
and statistics has confirmed that the research decisions made are reasonable
and “sound good” but that an expert in time series analysis
should be consulted. A thorough literature review did not help in this
regards and
at this point advice from a specialist in this type of statistical analysis
is important to confirm whether a more powerful or less biased statistical
procedure is available and whether the procedure employed is appropriate.
Introducing a new perspective of astrology has introduced statistical issues
that are not
often encountered.
In
addition to replicating this analysis with the Low
Yield, Low Risk AstroSignature, forecasts based on
the individual variables used in the AstroSignature
will be helpful in determining which factors are most responsible for
the
positive
correlations of predicted and actual gold prices. In both of the AstroSignatures
of the gold forecast option of the Sirius software, a heavy weight is
given to Sun and Jupiter in 7th harmonic aspects.
Because
the software allows
weighting of each astrological factor, an AstroSignature can be developed
that accurately
reflects the theoretical assumptions of the researcher. However, a
problem with some earlier research in astrology that
found positive relationships
through exploratory research, the findings were not always consistent
with theoretical
expectations and the AstroSignatures were complex and inconsistent.
For
example, the works of Mitchell Gibson, Anne Parker,
and Mark Urban-Lurain
derive AstroSignatures
that do not closely match an expected AstroSignature based on theory.
These researchers are pioneers in striving to determine
if astrology is capable
of producing measurable effects and their works are important stepping
stones on the path, but at some point research most likely will need
to have solid
theoretical underpinnings and produce simple and elegant results
if the findings are to be duplicated in future studies.
Otherwise one can simply
go round-and-round
conducting 1,000 studies to find .001 significance and thus confirming
that the family-wise probability is 1.0 when one has attempted a
sufficient
number
of hypotheses! In this study a fairly elegant formula that is consonant
with theoretical expectations has been found to predict economic
behavior.
This
finding therefore needs to be taken seriously as a possible step
towards the
discovery of a measurable astrological effect, and at present may
be one of the most positive steps forward in a scientific
form of astrology. Furthermore,
the findings of this study confirm the findings of other exploratory
research and pilot studies by the author that suggest that harmonic
astrological patterns
may produce measurable effects. Although this step forward in astrological
research may be very important and possibly open a door to a new
technology, enthusiasm for finding measurable effects of astrology
appears to be low among
astrologers as well as non-astrologers and discoveries beyond the
scope of what people perceive as possible are naturally met with
reluctance, and consequently
further development based on these promising results may develop
slowly. However, eventually this research thread will be continued
and gradually we may know
whether measurable astrological effects exist.
|
![]() Copyright © Cosmic
Patterns. All Rights Reserved Created
Copyright © Cosmic
Patterns. All Rights Reserved Created