ABSTRACT:
Michel
Gauquelin’s highly controversial and disputed
claim that eminent professionals are more likely
to be born when planets occupy particular areas in
the sky in their diurnal cycle has to date not been
successfully replicated according to some skeptical
reviewers of his research. As a first step in reassessing
the validity of Gauquelin’s theory, the diurnal
distribution of Mars, Jupiter, and Saturn in the
data collected by Gauquelin is reanalyzed using software
that was unavailable at the time that the Gauquelin
studies were conducted. The results of this reanalysis
of the data suggest that the “plus zones” appear
to be much smaller than the plus zones suggested
by Gauquelin. The theory of golden means proposed
by Theodor Landscheidt as a basis for the planetary
effects by Gauquelin is mildly supported by the data.
Measurement in Placidan arc sectors provided more
significant results than measurement in zodiac longitude
or right ascension. For future research involving
hypothesis tests it is suggested that smaller plus
zone areas than specified by Gauquelin be specified
in the hypothesis test. Keywords:
Astrology –– Gauquelin –– Mars
Effect –– Landscheidt –– golden
ratio
INTRODUCTION: Planets
rise in the east, culminate (reach their highest
point in the sky above the horizon), set
in the west, anti-culminate (reach their lowest point
in the sky below the horizon), and then rise again
in a cycle that on average is about 24 hours in length. As with the Sun, the time from rising to setting
varies considerably depending on the geographic latitude
and also the declination (angular distance from the
celestial equator) of the planet. Because traditional
astrological associations with the planet Mars include
qualities like aggression and physical prowess, and
because planets traditionally were considered “strong” in
a person’s life if located near the rising
or culminating positions at birth, Michel Gauquelin
proposed that an eminent athlete is more likely to
be born at that time of the day just after Mars rises
and culminates.
In some
of Gauquelin’s studies he divided
the sky into 12 sections and in other studies he
divided the sky into 36 sectors. When a planet rises,
it enters the first sector regardless
of whether there 12 or 36 sectors. If
12 sectors are used, then the planet enters the fourth
sector
when it
culminates, enters the seventh sector when it sets
and enters the tenth sector when it anti-culminates.
Each of the quadrants is divided into 3 sections,
which are calculated with a method sometimes referred
to as Placidian arcs or declinational circles, and
a planet occupies each of the three sectors in each
quadrant for approximately the same duration of time.
Gauquelin
proposed that sectors 1 and 4 (just after rising
and culminating) are the areas in the planet’s
diurnal motion when its effect is most strongly felt.
Eminent athletes, for example, are more likely to
be born when Mars is in sectors 1 and 4. According
to astrological lore, Mars is the planet of action
and power, so an association of outstanding athletic
performance with the planetary position of Mars is
similar to astrological ideas, although astrologers
generally do not measure planetary positions using
Placidian arcs nor do they usually associate the
areas just after rising and culminating as areas
where a planet is strong. Therefore, Gauquelin’s
theory of sensitive diurnal sectors has some affinities
with traditional astrological theory but also departs
from astrological tradition in some ways as well.
When 36 sectors are used, sector 1 in the 12-sector
division becomes sectors 1 to 3, and sector 4 in
the 12-sector division becomes sectors 10 to 12.
The sector just preceding these sectors, 36, and
9, were also regarded by Gauquelin in his later studies
as being important. (Gauquelin, 1988).
Gauquelin
proposed that eminence in various professional
fields is associated with different planets in “plus
zones” as shown in Table 1. In this table “+” indicates
that the planet is likely to be in sectors 1 and
4, and to a lesser extent the opposite sectors of
7 and 10, in the 12-sector division of the diurnal
cycle. Similarly, “-“ indicates that
the planet is less likely to be in one of these sectors
for this professional group. For example, according
to Gauquelin, scientists are more likely to have
Saturn and less likely to have Jupiter in one of
these sectors than people in a different profession.
Note that more specifically Gauquelin proposed that
the tendency for these planet placements occurs only
in eminent scientists, that is, scientists who have
achieved eminence or prominence in their field. 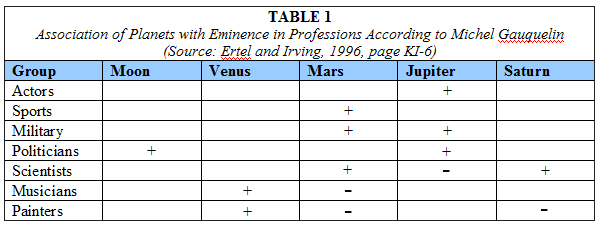
The
data presented in Table 1 present a simple and
elegant astrological theory. Each
profession has its own unique “astrological
signature”. An actor is more likely to have
the planet Jupiter in a “plus zone” as
Gauquelin referred to sectors 1 and 4 of the 12-sector
division of the diurnal sky.
For
sports champions the planet is Mars, for military
leaders both planets
Mars and Jupiter, and so on. Also, the planets
correspond well with the attributes of planets
traditionally associated with the behaviors involved
in these professions. For example, the planet
Jupiter is expansive, optimistic, and gregarious
according
to astrologers and is associated with professions
that involve expressiveness or grandeur: actors,
military leaders, and notable politicians. Saturn
is a planet associated astrologically with introversion,
focus, and severity, and scientists have a combined
effect of Jupiter excluded from a plus zone and
Saturn in a plus zone which hypothetically increases
the focused attention required of scientists.
The Moon is associated with moods and establishing
a bond with the public through a public sentiment
and mood, a helpful quality for politicians.
Venus,
which in myth and astrological symbolism is a
planet of beauty and grace, appears more often
in plus
zones for painters.
The
simplicity of Gauquelin’s theory and
the close correspondence of appropriate planets
with professions from the point of view of astrological
tradition are attractive features for believers
in astrology, and is disconcerting for skeptics
of astrology if his findings can be replicated
in later studies. Gauquelin’s findings became
a source of controversy and seemingly endless debate,
and many non-believers have concluded that there
are methodological problems with Gauquelin’s
studies. (Dean, 2002; Dean, 2003, Nienhuys, 1997).
REANALYSIS
OF THE GAUQUELIN DATA:
Gauquelin
analyzed the Mars sectors in the birth charts
of 2,088 eminent sports champions (Gauquelin,
1988). He also analyzed the Mars sectors in the
charts of 24,961 charts of a control group and
he presents a Chi Square statistical test that
compares the frequency of the occurrence of Mars
in sectors 1 (just after rising) and 4 (just after
culminating) of the12-sector division of the diurnal
circle between sports champions and the control
group. The statistical significance of the Chi
Square test is p<.001. (Gauquelin, 1988, page
37). The simplicity of the hypothesis (Mars occurs
more often in diurnal sectors 1 and 4 in eminent
sports champions than in other charts) and the
high degree of statistical significance suggests
that Gauquelin had made a breakthrough discovery.
However, a visual inspection of the distribution
of planetary position in diurnal sectors reveals
a more complex distribution of Mars in the diurnal
sectors than one may have suspected from reading
the research reports of Gauquelin. In Figure 1
is a graph of the planet Mars in 12 sectors and
72 sectors for sports champions. The 72 sector
division shows variations in frequencies across
6 “sub-sectors” of each of the 12 sectors
that Gauquelin analyzed in his study. The data
were obtained from two different sources: astrologer
Lee Lehman who had obtained the data directly from
Francoise Gauquelin (the wife of Michel Gauquelin
and a co-researcher with Michel Gauquelin) and
also available from the website www.cura.fr The
data from Lee Lehman and the website were compared
and found to be virtually identical. These data
are also provided in commercial software (Cosmic
Patterns, 2009). There are 2,536 sports champions
in this analysis as compared to 2,088 sports champions
in the study conducted by Gauquelin cited above
in 1988. The continued work by the Gauquelins added
over 400 additional sports champions, an increase
of 21%, to the data collection since the study
in 1988.


Fig. 1:
Mars in 12-sector and 72-sector Placidian Arc
Sectors for 2,536 Sports Champions
In
this paper we often refer to each of the sectors
analyzed by Gauquelin as “Placidian
arc sectors” to distinguish them from other
ways of measuring diurnal sectors which are discussed
later in this paper.
The
12-sector graph in Figure 1 shows the peaks in
sectors 1 and 4 as expected according to Gauquelin’s
theory. The 12-sector graph in Figure 1 is extremely
similar to the 12-sector graph of Mars for sports
champions in the original Gauquelin research (Ertel
and Irving, 1996, page KI-7). The relative heights
of each sector are nearly identical to those obtained
by Gauquelin. Slight differences between the graph
produced by Gauquelin and the graph given in Figure
1 are line graph is slightly higher at sectors
8 and 11 in Figure 1 than in the graph given by
Gauquelin. Given that there are 21% more sports
champions in the new analysis, the overall striking
similarity in graphs indicates that the additional
sports champions did not alter the basic distribution
of Mars in Placidian arc sectors found in Gauquelin’s
original study and that the calculation of planets
in Placidian arc sectors in this study agrees with
the calculation method used by Gauquelin.
The
72-sector graph indicates that the distribution
of Mars in sectors 1 and 4 of the 12-sector analysis
is not equally distributed in these “plus
zones”. By dividing the 360 degrees of the
diurnal path of Mars in 72 sectors of 5 degrees
for 2,536 champions an average of about 35 sports
champions per sector is obtained. If, for example,
180 sectors of 3 degrees is used, an average of
about 14 sports champions per sector is obtained
and consequently there would be much more random
fluctuation in scores due to the small average
number of 14 subjects per sector. The choice of
72 sectors was chosen to give a more detailed view
of the distribution of Mars but without having
too much random fluctuation in scores due to the
smaller average number of data for each sector.
The
72-sector graph in Figure 1 shows that there
are rather narrow and sharp peaks that account
for the peaks in the 12-sector graph. Rather than
a relatively high occurrence of Mars equally though
the first and fourth sectors of the 12-sector graph,
the 72-sector graph reveals sharp peaks occur towards
the end of these sectors. The first peak in the
72-sector graph is actually closer to the second
sector in the 12-sector graph! However, the graph
drops quickly after this peak and consequently
the total number of subjects is greater in sector
1 rather than sector 2 in the 12-sector graph.
Interestingly, a similar phenomenon occurs in sector
4 of the 12-sector graph. The actual peak shown
in the 72-sector graph is between sectors 4 and
5 in the 12-sector graph, and, similar to the first
peak, the decline after the peak is steep. The
overall pattern of these two peaks is extremely
similar: two small peaks precede them followed
by a steep decline. In this paper we will not analyze
all of these similarities in the peaks; we will
focus simply on the fact that the detailed distribution
of planets in the 72-sector graphs suggests that
the actual “plus zones” are slightly
more complex and narrower than the plus zones proposed
by Gauquelin. Rather than visualizing the plus
zone as a span of about 1/12 of the circle just
above the eastern horizon and 1/12 of a circle
just upper culmination, the 72-sector graph in
Figure
1 suggests a peaking late in these sectors
followed by a sharp decline.
The observation of variation in the Gauquelin
sectors was noted by Theodor Landscheidt (Landscheidt,
1989). Landscheidt proposed that the peaks occur
at golden ratio points along the diurnal path of
a planet. The golden ratio is significant in many
biological processes and has highly interesting
mathematical properties (Livio, 2003). A mechanism
by which the golden ratio or any other astrological
variable could be significant has not yet been
clearly formulated but nevertheless Landscheidt
is extrapolating a concept that is useful in other
areas of science to the domain of astrology. If
this extrapolation is validated by future research,
a mechanism by which it may operate can be pursued.
As stated earlier, the lack of supporting scientific
literature and the lack of an agreed upon mechanism
by which astrological influences operate suggest
that any astrological hypothesis be met with skepticism,
and rigorous and careful testing of the hypothesis
is required. In this initial attempt to verify
the theories of Gauquelin and Landscheidt, we do
confirm the observation of Landscheidt that the
distribution of Mars in plus zones may correspond
to golden ratio points, as described below. The
information provided below was determined by carefully
analyzing the information give by Landscheidt,
and is arguably a more detailed and systematic
in presentation than the one given by Landscheidt.
The
golden ratio is approximately 0.618, which is
equivalent to approximately 222.5 degrees of
the 360 degrees of a circle. Because Gauquelin
used rising, culminating, setting, and anti-culminating
points and these points are clearly defined astronomically,
we can measure an angle of 222.5 degrees from any
of these four points. However, the setting point
is opposite the rising point and we will refer
to two points that are opposite each other as an
axis. Similarly the culminating and anti-culminating
points lie on an axis. Furthermore we can measure
in either a clockwise or counter-clockwise direction.
The following angular distances therefore are golden
mean points in relationship to the rising-setting
axis measured in a clockwise direction, which is
the direction in which planets travel in their
diurnal motion and is also the order in which Gauquelin
ordered sectors: 225.5 (.618 x 360), 137.5 (.328
x 360), 42.5 (.618 x 360 + 180), and 317.5 (.328
x 360 + 180). The addition of 180 is the measurement
from the setting point. Note that 42.5 and 225.5
lie on an axis as do 137.5 and 317.5. Therefore
there are two golden mean axes from the rising
point and setting point: 42.5 degrees and 137.5
degrees. The 42.5 degree axis consists of the golden
ratio points based on the golden ratio of .618
and 137.5 is based on the “minor” golden
ratio of .328.
Landscheidt also hypothesized that the golden
ratio point from rising to setting, setting to
rising, culminating to anti-culminating, or anti-culminating
to culminating could also be important. To make
this idea concrete, imagine that for some reason
the power or influence of the Sun in some way reaches
its maximum (or minimum) when it reaches the golden
ratio point in its travel from rising to setting.
Maximum (or minimum) points also occur measured
from setting to rising, culminating to anti-culminating,
and anti-culminating to culminating. These golden
ratio points are in addition to the 42.5 degree
and 137.5 ratio points discussed above, which are
golden ratio points in relationship to one complete
diurnal cycle. These additional golden ratio points
measured from the rising point and setting point
add two more axes: at 68.8 degrees and 111.2 degrees
(and the points opposite to these). The angle of
111.2 degrees can be regarded as more closely related
to the golden ratio (180 x .618) and the angle
of 68.8 degrees as more closely related to the
minor golden ratio (180 x .382).
To summarize, there are four golden ratio axes
according to Landscheidt and these are:
42.5
and 222.5: major golden ratio of 360 degrees
137.5 and 317.5: minor golden ratio of 360 degrees
111.2 and 291.2: major golden ratio of 180 degrees
68.8 and 248.8: minor golden ratio of 180 degrees
In
addition to the above four axes, Landscheidt
proposes that the axes that are 90 degrees to
these
axes are also significant, resulting in 4 sets
of “crosses” rather than axes that
are significant.
Landscheidt also suggests that golden ratios of
90 degree sections are also important, so that
55.6 degrees (90 * .618) and 34.4 degrees (90*.382)
and the other three points forming crosses with
these points may also be significant. In Table
2 is a summary of all of the angular distances
that may be golden ratio points in the first 90
degrees from a given point according to Landscheidt.
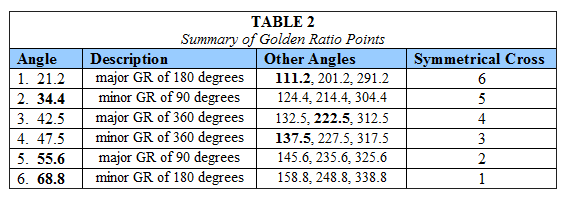
In
Table 2 “GR” indicates
golden ratio. The number in bold is the value calculated
from the description of the golden ratio. For example,
111.2 degrees is the major golden ratio of 180
degrees.. The other angles are multiples of 90
degrees from the calculated value. The symmetrical
cross has an angular distance that is equidistant
from the starting point on the other half of the
circle. For example, 338.8 (in cross #6) degrees
is 21.2 degrees from the starting point so it is
a symmetrical cross with cross #1, which includes
the value 21.2 as one of its four points. All four
points in a symmetrical cross are symmetrical (equidistant
from the starting point) of a point in the cross
it is symmetrical to.
There are a total of six golden ratio crosses
for a total of 24 golden ratio points. On average,
there is a golden ratio point every 15 degrees.
With a large number of golden ratio points, one
can argue that it is almost certain that one can
find some correspondence of peaks in the diurnal
placement of Mars in the charts of sports champions
with golden ratio points. On the other hand, we
do expect that all four points of a cross have
a similar effect, and other consistencies in the
use of golden ratios (using major rather than minor
gold ratios, for example) can be used to help provide
a consistent basis for associating golden ratios
with peaks in the graph of diurnal planetary positions
of particular planets at the time of birth of people
who have achieved eminence in a particular profession.
For
the placement of Mars for sports champions Landscheidt
associates GR cross # 3 with lows and
GR cross # 1 with highs in the graph. In other
words, Landscheidt proposes that eminent sports
champions are less likely to be born when Mars
is at the 360-degree major golden ratio point,
and they are more likely to be born when Mars is
at the 180-degree major ratio point. In the 72-sector
graph the large up arrows are 180-degree GR points,
the small up arrows are 90-degree GR points, and
the down arrows are 360-degree major GR points.
Therefore, according to Landscheidt’s theory,
the large up arrows should indicate highs in the
graph and the down arrows should indicate lows
in the graph.
In
the first half of the graph in Figure 1, we see
that the two peaks do coincide with the 180-degree
GR points (indicated by large up arrows in the
72-sector graph in Figure 1). The 360-degree GR
points (down arrows in the graph) do not obviously
coincide with troughs as Landscheidt suggests that
they would. An alternative theory to Landscheidt’s
is that 180-degree GR points are associated with
peaks and 90-degree GR points (small up arrows
in the graph) are associated with the troughs.
If we imagine a gradual wave with a sinusoidal
shape reaching its highest point where the large
up arrows occur in this graph, and reaching its
lowest point where the small up arrows occur in
the graph, it fits the overall distribution of
Mars in the first half of the graph fairly well.
In
both the 72-sector graph and the 12 sector graph
in Figure 1 the first half of the line has
two clear peaks and the second half of the line
is fairly flat. The first half of the line shows
how often Mars was above the horizon at the time
of birth of the sports champions and the second
half represents the placement of Mars below the
horizon. Because the graph of Mars below the horizon
is fairly flat, an attempt to associate peaks and
troughs in the graph with golden ratio points is
difficult, and it appears that the placement of
Mars below the horizon is fairly random. Also,
in some of Gauquelin’s studies (e.g. Gauquelin,
1988) only Mars above the horizon was analyzed.
Throughout the rest of the paper we will focus
primarily on planets above the horizon, i.e. the
first half of the graph.
Another consideration in analyzing the diurnal
position of planets is the method for measuring
the planet position in the diurnal cycle. Gauquelin
used a method that we are referring to as Placidian
arcs. Astrologers typically project planet positions
onto the ecliptic plane and the resulting positions
are known as ecliptic positions or zodiac longitude
positions. Less used by astrologers but more often
used by astronomers are positions projected on
the equatorial plane and these positions are known
as right ascension positions. After producing graphs
in longitude and right ascension measured from
both the rising point and the culminating point
and comparing these to various golden ratio positions,
only the zodiac longitude positions appeared to
provide a good correspondence with the peaks and
troughs in the graph of Mars for sports champions.
However, with 24 golden ratio points and the rather
subjective evaluation of agreement of these points
with peaks and troughs, other conclusions may be
possible. Visual tools are vitally important for
initial investigations and exploratory research.
We are not presenting here the many graphs that
were studied that did not appear to show good correspondence
with the peaks and troughs in the graph of Mars.
Given in Figure 2 is the graph of Mars in zodiac
longitude with the same golden ratio points indicated
that are in the graph using Placidian arcs Figure
1. Also included in Figure 2 is the graph using
Placidian arcs which was already presented in Figure
1, but is included in Figure 2 to assist in visual
comparison of measurement using zodiac longitude
and Placidian arcs.
Zodiac Longitude

Placidian
Arcs

Fig.
2: Mars in 72-sector Zodiac Longitude and
Placidian Arc Sectors for 2,536 Sports Champions
A visual comparison of the zodiac
longitude (top) graph and the Placidian arc (bottom)
graph appears to show a closer correspondence of
highs with up arrows in the zodiac longitude graph.
The first 6 of the 8 up arrows in the zodiac longitude
graph appear to point to highs, although visual
inspection is somewhat subjective. In both graphs
the first peak is indicated by the first large
up arrow, but in the graph using Placidian arcs
the first small up arrow does not point to a peak
as clearly as in the zodiac longitude graph.
From
the above observations we can draw a tentative
conclusion that Lanscheidt’s theory of golden
ratio points provides a better correspondence with
highs in the graph than Gauquelin’s theory.
We also conclude that both zodiac longitude and
Placidian arcs may be viable measurement systems.
Studying the diurnal distribution of planets in
other professions can help confirm whether our
tentative conclusions continue to be supported.
Rather than relying exclusively on hypothesis testing
and quantitative analysis, exploring the data by
studying graphs provides insights that can provide
a basis for hypotheses that are more likely to
be supported in hypothesis tests.
According to Gauquelin, military leaders also
have Mars (as well as Jupiter) appearing in plus
zones more often than can be expected by chance.
Given in Figure 3 is the distribution of Mars in
Placidian arcs and Zodiac Longitude for military
leaders.
Zodiac Longitude

Placidian Arcs

Fig.
3:
Mars in 72-sector Zodiac Longitude and Placidian
Arc Sectors for 3.393 Military Leaders
Although there appears to be some
relationship of the golden ratio points with peaks
and troughs in the graphs in Table 3, the association
is not entirely clear and consistent, although
the first three arrows (large up arrow, down arrow,
and small up arrow) in the Placidian arc graph
do line up nicely with the first peak, first trough
and second peak.
We
may be tempted to conclude that the weak support
for the “Mars effect” in military leaders
is a strong indication that the supposed Mars effect
does not exist. However, the expectation that Mars
will be prominent in the charts of athletes may
be more theoretically sound than the expectation
that Mars will be prominent in the charts of military
leaders. Although a military leader superficially
would seem to be a good symbol of the aggressive
nature of Mars, the tendency of modern astrologers
is to see planetary effects as being related to
basic principles that do not necessarily manifest
in obvious ways. In other words, Mars may not be
associated with warriors literally but rather with
strong motivation and drive. Although military
leaders are likely to be more involved with combat
and war, it is not as clear that they are more
motivated and energetic than professionals in other
fields. In Gauquelin’s later research he
focused on people who were described in their biographies
in ways that correspond to the astrological attributes
of the planet. For example, a military leader described
as energetic and aggressive would be included in
the group of military leaders and a military leader
not described this way in the biography would be
removed from this group. Therefore, Gauquelin was
also inclined to reanalyze the data with an interest
in personality traits rather than a more superficial
association of a profession with the planet. Given
this concern, we next look at Saturn in the charts
of eminent scientists. Assuming that eminent scientists
are more likely to be highly focused, sometimes
working quietly, analyzing and studying situations
in solitude, the expectation is that scientists
are more Saturnian than the average person. We
are only speculating here, but also Gauquelin identified
the planet Saturn as being in the plus zones for
scientists.
Zodiac Longitude

Placidian Arcs

Fig. 4:
Saturn in 72-sector Zodiac Longitude
and Placidian Arc Sectors for 3.646 Scientists
The
two graphs for scientists in Figure 4 appear
to mildly confirm Landscheidt’s
theory. In both graphs the first arrow points to
a high, the first down arrow points reasonably
close to a low, and the second up arrow points
to a fairly high point. For the Placidian arcs
graph, you can imagine a smooth wave that has a
sinusoidal quality reaching a high peak where the
large up arrows are and a smaller peak where the
low arrows are, the resulting graph appears to
have a close similarity to the line graph, especially
for the first half of the graph.
For our final example of diurnal distribution
of planets we will look at Jupiter in the charts
of politicians. Gauquelin found that Jupiter appeared
in plus zones for politicians. As with Saturn and
scientists, the association of Jupiter with politicians
would seem to be very appropriate. It seems reasonable
to expect that most politicians spend time with
situations that involve many people, they deal
with large, broad issues, and the travel, dinners,
campaigns, and other activities associated with
politics involve reaching out, traveling, and dealing
more with large concepts more than minute technical
details that, for example, a technician would be
more likely to be occupied with. In Figure 5 is
given the distribution of Jupiter in Placidian
arc sectors. The distribution in zodiac longitude
is not included because the association with golden
ratio points was weak, and we shall focus on Placidian
arcs as the most strongly supported measurement
system.

Fig. 5:
Jupiter in 72-sector Placidian Arc Sectors for
1,318 Politicians
Just as with scientists, the first
three arrows (first large up arrow, first down
arrow, and first small up arrow) fit very well
with the graph. The second down arrow, however,
does not point to a low, and in some of the analyses
above, the down arrows also do not consistently
line up with lows in the graph. Again we find that
the up arrows point to highs more consistently
in the first half of the graph.
CONCLUSION
FROM THE VISUAL INSPECTION OF THE GRAPHS:
From the above graphs the most consistent theme
is that the first four or five of the large up
arrows (180-degree major GR points) indicate highs,
and the small up arrows (90-degree major GR points)
also indicate highs but highs that are not as pronounced
as for the 180-degree major GR points. Placidian
arcs appear work as well, or better, than using
either zodiac longitude or right ascension. From
the visual inspection of these graphs we conclude
a modification to the definition of plus zones
as defined by Gauquelin to plus zones that conform
more closely to those specified by Landscheidt
is likely to produce results in studies with greater
statistical significance than using the plus zones
as defined by Gauquelin.
The visual inspection of graphs focused on the
planets Mars, Jupiter, and Saturn and future research
can analyze the distribution of other planets in
the diurnal cycle.
CONCLUSIONS:
Summarized below are important conclusions from
the research presented in this paper.
1. Plus
zones smaller than those defined by Gauquelin: The reanalysis of the eminent athletes data collected
by Gauquelin indicated that the plus zones are
four to five sectors in the 72 sector division
after rising and culminating.
2. The
golden ratio theory of Landscheidt is mildly
supported: Landscheidt’s theory of golden
ratios indicates that plus zones are smaller than
the size indicated by Gauquelin and this was confirmed,
but the golden ratio points did not consistently
identify peaks in the data.
3. Importance
of different astronomical measurement systems: Placidian arc sectors appear to correspond
to expected peaks in the data better than measurement
in zodiac longitude and right ascension.
4. Importance
of visual tools in the early model-building
phase of astrological theory: Popular astrological
theories have generally failed to be supported
by astrological research (Dean, 1977) and even
some astrologers have concluded that most astrological
assertions may be incapable of being validated
by empirical research (Cornelius, 2002). Therefore,
attempts to validate astrology can perhaps benefit
from exploratory methods such as analyzing graphs
of data rather than only analyzing the statistical
results of hypothesis tests. Creative insights
such as the importance of golden ratios proposed
by Landscheidt may provide a basis for future research,
and visual tools can be helpful in assessing the
relevance of these new concepts.
ACKNOWLEDGEMENT:
We are grateful for the guidance and technical
suggestions of Dr. Monika Ardelt, Sociology Department,
University of Florida.
REFERENCES
Cornelius, Geoffrey. (2003). The
Moment of Astrology.
Bournemouth, England: The Wessex Astrologer.
Cosmic Patterns Software. (2009) Sirius
software,
Version 1.2. Gainesville, FL: Cosmic Patterns Software
Dean, Geoffrey. (1977). Recent
Advances in Natal Astrology: A Critical
Review 1900-1976. England:
The Astrological Association.
Dean, Geffrey (2002). Is
the Mars effect a social effect? A re-analysis of the Gauquelin data suggests
that hitherto baffling planetary effects may be
simple social effects in disguise. Skeptical
Inquirer, May 2002 v26 i3, pp 33(6)
Dean, Geffrey (2003). Response to Ertel. (Follow-up).
Skeptical Inquirer, Jan-Feb 2003 v27 i1 pp 59(2)
Ertel,Suitbert & Irving,
Kenneith. (1996). The Tenacious Mars Effect. Londong: The Urania
Trust.
Gauquelin, Michel. (1988). Is there a Mars Effect?
Journal of Scientific Exploration, Vol 2, No 1,
pp 29-51
Landscheidt, Theodor. (1989). Sun-Earth-Man: A
Mesh of Cosmic Oscillations. London: Urania Trust
Livio, Mario. 2003. The
Golden Ratio: The Story of Phi, The World's
Most Astonishing Number New
York: Random House
Nienhuys, Jan Willem. (1997). The Mars effect
in retrospect. Skeptical Inquirer. Nov-Dec 1997,
v21, n6, p24(6)
|
![]() Copyright © Cosmic
Patterns. All Rights Reserved Created
Copyright © Cosmic
Patterns. All Rights Reserved Created