|
Note: This article combines information presented in the article “Cosmic Cybernetic Influences on the Development of Culture: A Post-Freudian Perspective” (http://astrosoftware.com/CosmicCybernetics.htm) and in the Sirius software program (http://AstroSoftware.com) I have not included quotations or references because over half of the article presented below is copied or adapted from these two sources. The material from these two sources is combined together here with additional material in order to present the relationship of Planet Mandalas, and the larger discipline of cosmic cybernetics, with fundamental theory in physics. The author is also the founder of the company that produces the Sirius program and is the author of the article, and permission to use these sources in this article has been obtained.
WHAT
ARE PLANET MANDALAS? Planet
mandalas are representations of the orbital motions
of planets. All of us are familiar with the
image of our solar system with the Sun in the middle
and the elliptical orbits of the planets shown as
ellipses of various sizes and proportions with Mercury
closest to the Sun, followed by Venus, and so on.
In a planet mandala one or more adjustments are made
to the representation of the elliptical orbit. One
of these adjustments is that the orbits may be
drawn
from the point of view of another planet,
such as the Earth. Imagine, for example, the path
of Mars from our point of view. When Mars is geocentrically
opposite the Sun, it is relatively very close to
us on Earth. When Mars is geocentrically in the same
direction as the Sun, it is relatively very far from
us. We can draw the apparent path of Mars from the
geocentric point of view, i.e. how Mars appears to
be moving if the Earth was stationary. In fact, as
discussed in a bit more detail below, this is exactly
what Kepler did in working out the path of the orbit
of Mars en route to his discovery of the 3 fundamental
laws of planetary motion. These changes in distance
from the Earth result in intriguing shapes which
tend to have some symmetry and have roughly a circular
boundary and therefore have been given the name “planet
mandalas” by the early pioneers in the computer
programming of planet mandalas, Neil Michelsen and
Mark Pottenger. One
may argue that drawing the apparent geocentric
orbits
of planets is not their real orbit. The real
orbit is the one that is observed from the perspective
from outer space looking at our solar system from
a distance, and therefore these geocentrically viewed
orbits are curious illusions. However, one can also
argue that absolute frames of reference are not always
possible ala relativity theory. Also, the apparent
magnitude of a star is just as important to us as
the absolute magnitude of a star. A may be many thousands
of times smaller than a galaxy but the galaxy may
be so far that it is not visible while the star appears
bright in our sky. Not only is a star-filled sky
aesthetically different from a complete black sky,
but the light radiation that reaches us is a different
phenomenon than light that does not reach us. From
a philosophical point of view, one can argue about
whether apparent geocentric orbits may be of any “real” importance,
but the fact is that these orbits are visually intriguing
and interesting than the heliocentric elliptical
orbit, which, in common parlance, is simply egg-shaped
with varying thicknesses and sizes of the egg depending
on the orbit of the celestial object. Another
adjustment to the drawing of the planet orbit is
that we can draw the orbit of 2 planets.
The orbit is drawn by calculating the daily positions
of the planets over some duration of time, which
can be as few as a few days or may span centuries.
On each day of the calculations a line is drawn directly
between the two planet positions. This line, of course,
shows the relationship of the planets to each other.
When one looks at a night sky and notices two objects
in roughly the same area of the sky, our eyes may
dart back and forth between the two objects or we
may instinctively draw an imaginary line between
the planets. This tendency of the human mind to “connect
the dots”, so to speak, is fundamental to our
concept of constellations, where we draw imaginary
pictures by drawing lines between the planets. These
imaginary lines of the constellations have no objective
reality and are simply a proclivity of the human
mind to find patterns. In drawing lines between the
daily positions of planets, however, we also can
see the changing relationship of the planets to each
other. By connecting the daily positions of the planets,
the planet mandala may become visually much more
intricate and in some cases beautiful. A
third adjustment that can be made to the representation
of the planetary orbit is to use color to represent
the third dimension of the planet’s orbit,
i.e. how far above or below the paper or computer
screen upon which the orbit is drawn the planet is
located. This is the Z coordinate in the rectangular
coordinate position of the planet. If one designates
a blue for the planet reaching its maximum north
z coordinate position and red for its maximum south
z coordinate position, and varying colors proportionate
to how far the planet is from a z coordinate position
of zero, then the color will be a mixture of red
and blue (purple) when the z coordinate position
is zero, and the color gradually having less red
and more blue as the z coordinate increases, and
gradually becoming less blue and more red as the
z coordinate decreases. Although this idea may seem
like an obvious way to show the varying levels of
the z coordinate, it had not been done until the
author programmed this feature as a feature in the
Sirius program which became available in May, 2008.
Progress in the study of planet mandalas is slow
because there has been little interest in them since
Kepler drew the first planet mandala in his classic
work, The New Astronomy (of course, he did not refer
to it as a planet mandala, but just simply as the
geocentric orbit of Mars). The addition of this color
gradient to the planet mandala results in the planet
mandala becoming much more stunning, even more dramatically
than I had anticipated. Another adjustment that can be made is to calculate
the planet positions at some other interval rather
than every day. Imagine calculating the position
of the Earth every 180 days for example. The positions
would be almost opposite each other when calculated
every 180 days but not perfectly opposition because
180 days is slightly less than half of 365.25 days.
Interesting patterns can emerge by periodically calculating
the planets. Another alternative to plotting planetary positions
is to plot some other attribute of the planet orbit
rather than its actual position. One can plot, for
example, a kind of radial graph that displays the
planet position by its speed. As the planet speed
increases, the planet position can be drawn further
from the center analogous to a kind of centrifugal
force as the apparent speed (or actual speed if the
heliocentric speed is used) changes, with greater
speed represented as a greater distance from the
center. Variations of this formula can handle retrograde
motion by either taking the absolute motion of the
speed or by considering maximum retrograde motion
as the slowest speed. These graphs are pictorial
representations of orbital motions rather than literal
graphs of planetary positions. These kinds of planet
mandalas were introduced in 2008 in the Sirius program,
and, like the usual planet mandalas, create intriguingly
beautiful shapes. In the Sirius software there are 8 different kinds
of planet mandalas. Some are geocentric, some are
heliocentric, some plot the position of one planet
and some plot two planets, and some are plots of
actual positions and others are graphs showing positions
related to planetary speed. For each kind of planet
mandala there are dozens of different mandalas that
can be chosen, and the user may select his/her own
planets, starting time for calculations, duration
of calculations, etc. In
this article I will discuss the relationship of
planet
mandalas to the work of physicists like
Stephen Wolfram and Ray Kruzweil, but first let’s
look at some images of planet mandalas. The reader
who is primarily interested in seeing planet mandalas
may be content to simply enjoy the following images
and skip the rest of this article. The reader who
is interested in the relationship of the work on
planet mandalas with fundamental theory in physics
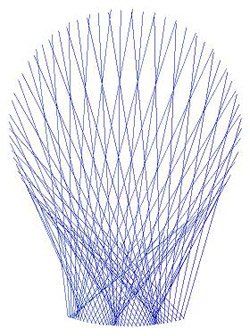
will benefit from reading this entire article. Planet Mandala Images Shown below are 16 planet mandalas. Although 16
planet mandalas may seem excessive, it does help
convey a sense of the range of possible shapes that
are possible. Even 16 images is not enough to give
a comprehensive view of the possibilities. There are many factors that affect the appearance
of the planet mandala in addition to the factors
mentioned above of the kind of planet mandala, planets
selected, duration of the calculations, and interval
between calculations. The starting date, level of
magnification, and even color selections affect the
appearance of the mandala as well. Planet mandalas reveal an exquisite
beauty in planetary orbits that has been largely
overlooked by the community of scientists as well
as artists. Planet mandalas are works of art created
by the movement of planets and appear to have elements
of shading, dynamic motion, sensitive symmetry,
and elegant design elements similar to what a very
skilled artist might produce but they are drawn
by planetary motions rather than human hands. Also note that in addition to viewing the completed
planet mandalas, as shown below, watching the planet
mandala being drawn can be equally fascinating.
There is one planet mandala in the Sirius program
called the Shiva Dance which many people find particularly
fascinating to watch. These animations can be saved
to file and uploaded, and we plan to upload the
Shiva Dance soon. The History of Planet Mandalas In
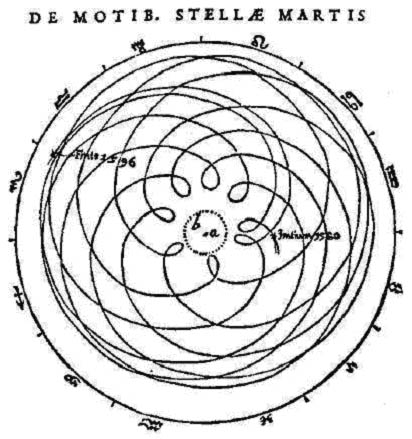
Kepler’s monumental work Astronomia Nova
(The New Astronomy) in 1609 Kepler described his
intensive work that gradually resulted in his discovery
of the elliptical orbits of planes the laws of
planetary motion. In this book he also has a drawing
of the orbit of Mars from the Earth’s point
of view. As
you can see, Kepler’s image
is extremely accurate. Note that these diagrams
show the actual path of Mars as seen geocentrically.
When Mars is opposition the Sun it is physically
much closer to Earth than when Mars is conjunct
the Sun. By holding the Earth stationary and plotting
the motion of Mars we obtain the diagram shown
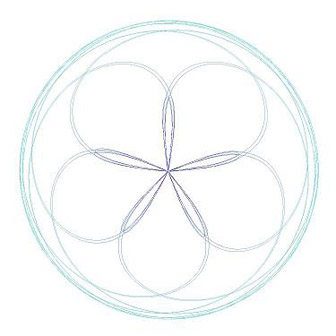
above. Even more intriguing is the path of Venus,
which produces a more symmetrical and easily identifiable
5-petaled shape. The
intriguing geocentric orbit of Mars was drawn
by Kepler as part of his intense and arduous work
in determining the laws of planetary motion. Kepler’s
laws of planetary motion explained very precisely
how the apparent position of Mars was a result
of its elliptical orbit around the Sun. The geocentric
orbit of Mars was not dwelled upon by later astronomers;
it was simply a step taken by Kepler in his work
towards discovering the laws of planetary motion.
In the 1970’s Neil Michelsen and Mark Pottenger,
two people involved in software development for
astrological purposes, became intrigued by these
shapes and they began programming them. The author
contacted Mark Pottenger regarding these planet
mandalas and Mark Pottenger generously shared his
knowledge, program source code, and all of his
work with planet mandalas. In developing the computer
software, I added a few new variations to the concept
of planet mandalas, the most important of which
may be the addition of color. The planet positions
that are plotted in most kinds of planet mandalas
are the actual planet positions in 3-dimensional
space, which is referred to as astronomers as rectangular
coordinates. The rectangular coordinates of a planet
are an x, y, and z coordinate positions in the
3 dimensions of space. The planet mandala plotted
on a flat surface like paper or a computer screen
is the x and y coordinates, and I added color to
represent the z coordinate. Predicting
the shape of a planet mandala from the planets
and time period selected is extremely
difficult, and in most cases impossible. Very often
one simply arbitrarily changes values like the
starting date, duration, and other factors, and
simply draws the image to see what it looks like.
Similarly, when I added color to represent the
third dimension in space, I was not sure what the
result would look like. The aesthetic effect of
color was more dramatic than I imagined it to be.
In the images shown earlier in this article you
can image how the images would look if not in color;
they are still beautiful but most people agree
that they are “flatter” and less dynamic
and inspiring than when the planet mandalas include
color to indicate the z coordinate. Planet mandalas may simply be a curious phenomenon
with no practical value or applications other than
perhaps to engender aesthetic and artistic appreciation
for the viewers of these images. However, there
is a powerful new movement in physics that has
an interesting parallel with the recent discovery
of planet mandalas: the new kind of physics of
Stephen Wolfram. A
NEW KIND OF SCIENCE Wolfram points out that previous to his work,
one expected the explanation for a complex system
to be very complex as well, but simple iterative
processes produce forms that are surprisingly complex.
The complex forms produced by a simple iterative
process cannot always be predicted. One must simply
run the iterative process on a computer and see
the results. Even to a genius in the field of mathematics
and physics such as Wolfram is often startled by
the resulting patterns produced by iterative processes. While
reading the book A New Kind of Science, I repeatedly
wondered how and where the iterative
processes that Wolfram supposes generate complex
systems exist. Cell division and growth patterns
are possibilities. One relatively unexplored “generator” or “engine” that
involves an iterative process are the motions of
planets. Planets travel on their paths in a seemingly
endless cycles and arrange themselves in various
configurations, as noted by astrologers throughout
the ages. Although astrology has failed thus far
to produce any scientifically verifiable results
and even some astrologers see astrological processes
as existing outside the realm of science, it is
possible that there is some unnoticed relationship
between planetary positions and terrestrial behavior
because the mechanism through which this relationship
operates may lie largely outside the domain of
both astrologers and scientists. Stephen
Wolfram’s work involves discrete
automata and planet mandalas involve the analysis
of elliptical orbits. The two processes are different
but similar in many respects. Both processes are
simple and both are processes are iterative. In
both cases complex and beautiful patterns are produced.
Planet mandalas and discrete automata also have
much in common with fractals. In all of these mathematical
calculations a relatively simple formula is calculated
iteratively, feeding back into the variables in
the formula results from the previous calculation.
Fractals have proven to have useful applications
in the determination of fracture lines in shattered
or cracked materials, weather prediction, and other
applications. Planet mandalas may, or may not,
prove to eventually be useful for practical applications. Note
that there are three distinguishing factors of
planet mandalas as compared to fractals and
cellular automata as they are typically calculated:
(1) The effects of the perturbations from other
planets causes each iteration of the calculations
to vary slightly from previous calculations, thus
resulting in slight variations in the pattern that
are drawn. In nature, patterns are not perfect.
For example, a sliced apple that shows the star-shaped
arrangement of the apple seeds reveals a 5-petaled
shape that is highly symmetric but of course not
perfectly symmetrical. Nature produces slight “disfigurements” or
imperfections as opposed to the pristine perfection
of a mathematical algorithm. In this regards planet
mandalas more closely resemble the shapes we see
in nature than most mathematical algorithms produce.
(2) Because planet mandalas are based on the calculation
of elliptical orbits rather than additive and multiplicative
functions, planet mandalas tend to have more rounded
and smoothed edges. Fractals and cellular automata
tend to produce shapes that are jagged and may
more closely resemble cracks in a ceramic or glass
material, while planet mandalas tend to produce
curved shapes more similar to the forms of living
things, both of the plant and animal life. (3)
Planet mandalas are based on an actual physical
phenomenon, the positions of planetary bodies.
Many of the formulae used in fractal theory and
in cellular automata are formula that a mathematician
thinks of but have not been identified with a physical
process. There may be exceptions to this rule but
the distinction remains valid in that all planet
mandalas are shapes based on a physical reality
but not all fractals cellular automata are based
on something that has been identified to exist
in nature. Stephen Wolfram states that he believes that iterative
functions play a vital role in biological development
and evolution. Given the facts provided in the
previous paragraph, planet mandalas may through
some as yet undiscovered process provide a basis
for these biological processes. At this stage of
research, we are simply noting similarities in
the development of mathematical and fundamental
theory in physics, and noting that there may be
further integration of these findings. Although
it may be premature to speculate too far at this
point, perhaps future findings in physics will
identify a mechanism whereby the movement of relatively
small and dense aggregations of matter (i.e. planets)
can act as the iterative functions to set patterns
for development within any part of the solar system.
Large aggregates of matter, whether they are solid,
liquid, or gas, are relatively rare. Planets, asteroids,
and other celestial objects in our solar system
are not crammed together like cars on a freeway.
There are relatively large expanses of space separating
especially the larger celestial objects (i.e. the
planets) in our solar system. Perhaps the arrangement
of these celestial objects and the intricate patterns
that they create, as revealed in planet mandalas,
create patterns which, like a great cosmic fractal,
can be relevant to the patterns in our lives. PATTERNS
AS THE FUNDAMENTAL BASIS OF PHYSICS In addition to the growing interest in fractals,
cellular automata, and other iterative functions,
there is another important movement in physics
is an emphasis on patterns as being fundamental.
Consider, for example, this statement by physicist
and inventor Ray Kurzweil: Norbert Weiner heralded a fundamental change in
focus from energy to information in his 1948 book
Cybernetics, and suggested that the transformation
of information, not energy, was the fundamental
building block for the Universe. If transformation of information is the fundamental
building block of the Universe, then we might think
that nature may be very efficient, rather than
highly inefficient, and use the placement of the
relatively rare planets, stars, and other celestial
objects as nodes or points for transferring information.
Again, we are making a very large leap from a general
conceptual model, but the positive results of the
research in cosmic cybernetics indicates that such
a leap may not be as large as we might otherwise
think that it is. In
the same article quoted above, Wolfram is discussing
his views of Wolfram’s book A New Kind of
Science and Kurzweil articulates his own view of
the essential basis of the universe, and this statement
sounds even closer to cosmic cybernetics than the
views of Weiner and Fredkin: …My own philosophy is that of a "patternist," which
one might consider appropriate for
a pattern recognition scientist. In my view,
the fundamental reality
in the world is not stuff, but patterns. If I ask the question, 'Who am I?' I could conclude
that, perhaps I am this stuff here, i.e., the ordered
and chaotic collection of molecules that comprise
my body and brain. However, the specific set of particles that comprise
my body and brain are completely different from
the atoms and molecules than comprised me only
a short while (on the order of weeks) ago. We know
that most of our cells are turned over in a matter
of weeks. Even those that persist longer (e.g.,
neurons) nonetheless change their component molecules
in a matter of weeks. So I am a completely different set of stuff than
I was a month ago. All that persists is the pattern
of organization of that stuff. The pattern changes
also, but slowly and in a continuum from my past
self. From this perspective I am rather like the
pattern that water makes in a stream as it rushes
past the rocks in its path. The actual molecules
(of water) change every millisecond, but the pattern
persists for hours or even years. Perhaps
it is a bit hyperbolic to go a step further and
state that energy and matter exist solely for
the purpose of supporting patterns. In any case,
patterns are fundamental according to Kurzweil,
and it may be that nature is far more efficient,
integrated, and elegant in the way that she creates,
supports, and maintains patterns than we had previously
thought, and that, for example, the positions of
celestial objects are “used” to sustain
patterns. The gorgeous planet mandalas, therefore,
do not seem like coincidences that just happen
to be created by celestial motions, but rather
as nodes in an informational network designed to
create these patterns. COSMIC
CYBERNETICS Other articles on this website discuss cosmic
cybernetics, a theory that is even further outside
the framework of scientific ideas than planet mandalas.
The positive results of statistical studies on
cosmic cybernetics, the case studies, and fairly
detailed theoretical developments within cosmic
cybernetics may eventually lead to replicable,
consistent findings. The reader is referred to
the list of articles by the author at http://astrosoftware.com/AstrologyArticle.htm
for further information. Cosmic cybernetics bears
some resemblance to the patterns provided by planet
mandalas in that the arrangement of planets are
considered relevant to our lives and behavior on
Earth. CONCLUSION:
THE MISSING LINK The work of Wolfram, Kurzweil, and other leading
physicists has much in common with the planetary
motions of celestial bodies and the resulting planet
mandalas produced by these orbits. The addition
of color to represent the Z coordinate of the planet
positions, a new discovery presented in this article
and in the Sirius software for the first time,
reveals a great depth, elegance, and beauty to
planet mandalas than had been found previously.
However, a direct mechanism through which planet
mandalas could affect behavior on Earth is unknown
at this time. Cosmic cybernetic theory posits that the position
of planetary bodies act as points at the crest
of waves marking wave lengths as viewed geocentrically.
If an angle of 72 degrees separates two planets,
then a 5th harmonic wave is considered to be emitted
at the speed of light towards Earth because 72
degrees is 1/5 of a circle. This theory is based
on anecdotal evidence, a modern revision of ancient
astrological lore, and statistical studies that
have shown promising, but not conclusive, results.
If a mechanism for the transmission of these waves
which in many regards are similar to electromagnetic
waves but are based on the placement of celestial
objects, is discovered in dark matter, quantum gravity,
or some other as yet undeveloped part of the fundamental
theories of physics, then cosmic cybernetics as
well as the practical importance of planet mandalas
in our lives could be firmly established. However,
there appears at this time to be no clear and direct
line of theoretical development that would supply
a theoretical basis for the practical relevance
of planet mandalas and the validity of cosmic cybernetic
theory. Without a theoretical basis it is possible
that even repeated and consistent replication of
studies that validate cosmic cybernetic theory
may tend to be ignored. Paradigm shifts can be
slow even when a theoretical basis is established,
and without a solid theoretical foundation, cosmic
cybernetics and the practical application of planet
mandalas for understanding behavior on Earth may
be very slow. The missing link, in short, is a
theoretical model that can tie cosmic cybernetic
theory to fundamental physics. Analogies and similarities
with cellular automata and the importance of patterns
is promising, but fall short of being a clear theoretical
foundation grounded in specific mathematical formulae. Nevertheless,
planet mandalas are important now as a bridge
between astronomy and art – a
curious intersection of aesthetics and astrophysics
that deserves attention for the inspiration and
wonder that they inspire. Further research in cosmic
cybernetics and the development of a theoretical
framework that is more solidly grounded in fundamental
physics are two important areas for future research
and development. |